Learning Algorithm
Intended audience: DATA SCIENTISTS DEVELOPERS ADMINISTRATORS
AO Platform: 4.3
Overview
This topic only relates to ML Models of Type: Bayesian Regression, Classification, and Clustering. For traditional ML Models, the Learning Algorithm page is not available; instead, the user will see an ML Algorithms section. See ML Algorithms > [Algorithm Name].
There are three key sections to the Learning Algorithm page:
Build Model - enter the Python code that will be used for the Bayesian ML Model.
Fitting Algorithm - select the type of Fitting Algorithm to use.
Parameters - update the properties to make adjustments to the Fitting Algorithm selected.
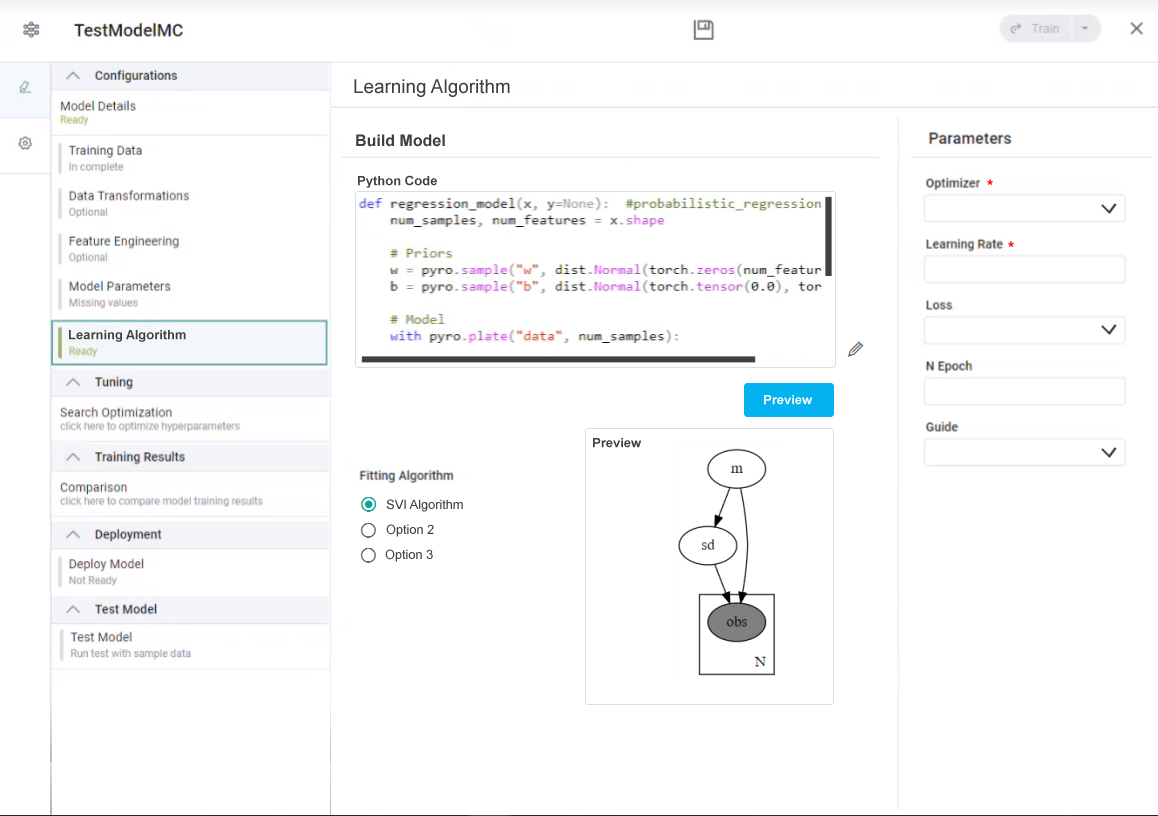
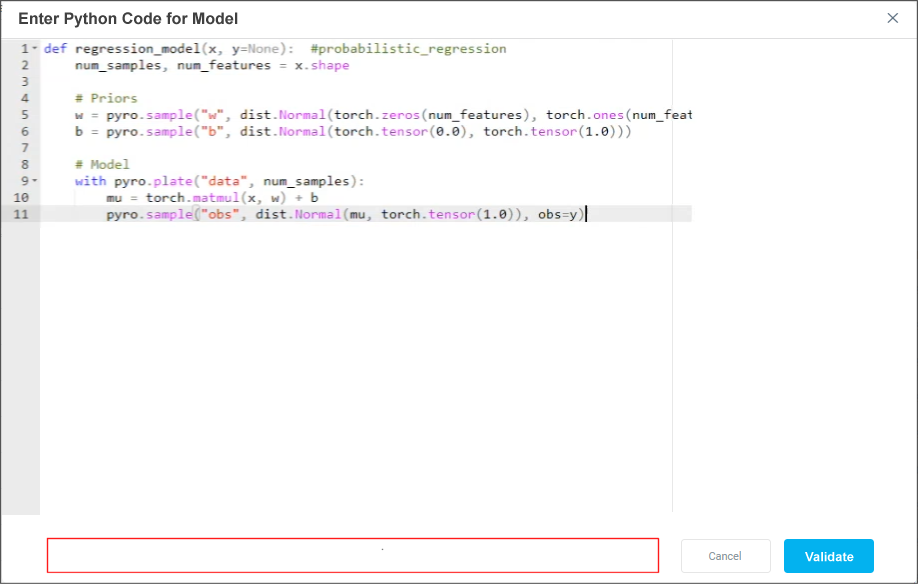
Build Model
This section is used to add the Python code for the Bayesian ML Model. Once the user clicks the Validate button, the code is validated, and if successful, the user can click the Preview button on the main page to view a graph illustrating the result of the code based on sample data. If the code does not validate successfully, an error message will be shown, and the Preview button will be greyed out.
Fitting Algorithm
The AO Platform is provided with the following Fitting Algorithms that can be used to create Bayesian ML Models.
Fitting Algorithms | Category | Description | Additional Documentation |
|---|---|---|---|
SVI Algorithm | Bayesian Inference. | Stochastic Variational Inference (SVI) is a method used for approximate Bayesian inference. It is particularly suitable for dealing with large-scale and complex probabilistic models. SVI approximates the posterior distribution by using a simpler and more manageable distribution called the mean-field Gaussian, achieved through optimization. This allows for faster and scalable Bayesian inference without the need for expensive and slow sampling methods. In simple terms, SVI acts like a clever shortcut that helps us solve big and complicated problems more easily, saving us time and effort while still providing useful answers. | |
MCMC Algorithm | Bayesian Inference. | Markov Chain Monte Carlo (MCMC) is a class of algorithms used for sampling from complex probability distributions, especially when direct sampling is infeasible. MCMC methods use a Markov chain, where the kernel plays a crucial role in updating the chain's state from one configuration to another. The kernel specifies the rules for proposing new candidate states given the current state of the Markov chain. These candidate states are then either accepted or rejected based on certain criteria, such as the Metropolis-Hastings acceptance rule. This iterative process helps the Markov chain converge towards the target distribution of interest | |
Maximum Likelihood Estimation (MLE) | Bayesian Inference. | In Bayesian statistics, Maximum Likelihood Estimation (MLE) is a method used to estimate the parameters of a statistical model by finding the values that maximize the likelihood function based on observed data. Unlike classical MLE, Bayesian MLE incorporates prior knowledge or beliefs about the parameters in the form of prior distributions. This allows Bayesian MLE to produce posterior distributions, which represent the updated beliefs about the parameters after observing the data. Bayesian MLE provides a framework to quantify uncertainty and make probabilistic inferences, making it a powerful tool for parameter estimation in various applications. |
Estimation Method
Select from available options in the dropdown, including: Mean, Median, Mode. For Regression based models, the value should be the Mean, and for classification-based models, the value should be Mode.
Parameters
All properties are prepopulated with default values - see links for each of the Fitting Algorithms in the table above.
